УЧЕБНАЯ КНИГА ПО ХИМИИДЛЯ УЧИТЕЛЕЙ СРЕДНИХ ШКОЛ,
|
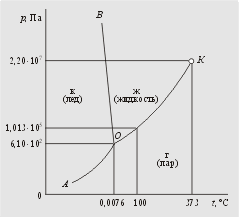 |
Рис. 5.11.
|
Теперь такую же прямую в виде стрелки
из той же точки проведите в вертикальном
направлении. Передвижение вдоль этой прямой (при
постоянной температуре) соответствует изменению
давления, которое не приводит к исчезновению
данной фазы и появлению другой.
Из той же точки (или любой другой того же поля)
можно провести прямую, направленную под любым
углом к осям координат. Передвижение вдоль такой
прямой до ее пересечения с кривой диаграммы
состояния означает возможность одновременного
изменения температуры и давления при условии
существования фазы данного поля. Таким образом,
на поле можно одновременно изменять температуру
и давление, не изменяя вида и числа фаз. Мы
говорим, что на поле система имеет две степени
свободы, по числу условий (температура и
давление), которые можно варьировать, не изменяя
вида и числа фаз или льда, или жидкости, или пара.
Число степеней свободы С – это число условий,
которые можно изменять в определенных пределах
без изменения числа и вида фаз.
Вы нагреваете воду от комнатной температуры,
предположим, до 80 °С в разные дни, когда
давление изменяется, но жидкость остается
жидкостью, хотя одновременно изменяются и
температура, и давление. В этих условиях система
имеет две степени свободы, т. е. С = 2.
Теперь поставьте точку, например, на кривой
диаграммы состояния равновесия между жидкостью
и паром (см. рис. 5.11). Жидкая вода и пар могут
находиться в равновесии при некоторых различных
температурах и давлениях, но каждой температуре
отвечает строго определенное давление, и,
наоборот, каждому давлению соответствует строго
определенная температура, при которой
сосуществуют две фазы. В этом случае мы говорим,
что система обладает одной степенью свободы, т. е.
С = 1.
Теперь остановимся на тройной точке О, в которой
при строго определенных температуре и давлении
сосуществуют в равновесии три фазы – лед,
жидкость и пар. Тройная точка характеризуется
единственным сочетанием температуры и давления,
поэтому-то температуру тройной точки и выбрали
как начало отсчета абсолютной температуры в
градусах Кельвина (273,16 К). Стоит незначительно
изменить давление или температуру, как одна из
фаз или сразу две переходят в другую, и система
становится двух- или однофазной – мы попадаем на
соответствующую кривую или поле. Одним словом, в
тройной точке система не имеет ни одной степени
свободы, т. е. С = 0.
При исследовании фазового состояния систем (не
только воды!) знание числа степеней свободы при
данных условиях очень важно, т. к. позволяет
предсказывать, сколько условий равновесия можно
изменять, не боясь появления новых фаз или
исчезновения имеющихся.
Число степеней свободы С равновесной
термодинамической системы подсчитывается по
правилу фаз Гиббса и равно числу компонентов
системы К минус число фаз Ф плюс число факторов n,
влияющих на равновесие:
С = К – Ф + n.
Здесь дана та формулировка правила фаз Гиббса,
которая приводится в строгой научной физической
или химической литературе, поэтому, наверное,
следует объяснить некоторые термины.
Компоненты системы – это те ее
составные части, которые могут быть выделены из
системы и могут существовать в индивидуальном
виде. Вода – компонент системы, но ионы воды или
другие ионы в водном растворе не считаются
компонентами, т. к. не могут быть выделены и не
существуют индивидуально. Чистая вода –
однокомпонентная система.
Если мы приготовим раствор поваренной соли NaCl в
воде, то система будет состоять из воды Н2О,
ионов натрия Na+ и хлорид-ионов Cl– (и,
конечно, ионов водорода Н+ и
гидроксид-ионов ОН–, образующихся в крайне
незначительном количестве при диссоциации воды).
Но система будет двухкомпонентной [Н2О + NaCl],
т. к. индивидуально можно выделить из раствора
жидкую воду и кристаллический хлорид натрия NaCl.
Факторы, влияющие на равновесие, –
это то, что мы называли раньше условиями
существования системы. Для рассмотренной
диаграммы состояния воды два фактора влияют на
образование и существование фаз – температура и
давление, n = 2. Формула правила фаз в этом
случае имеет вид:
С = К – Ф + 2.
В большинстве случаев в лабораторной работе проводят эксперименты при постоянном (атмосферном) давлении, поэтому только температура будет играть роль фактора, влияющего на равновесие, т. е. n = 1. Формула правила фаз в этом случае такова:
С = К – Ф + 1.
В последнее время обнаружено влияние
электромагнитного и гравитационного полей и
многих других факторов на равновесие. Но в
обычной научной работе эти факторы не
учитываются.
Сейчас выполним следующий мысленный
эксперимент, хотя его очень просто проделать
реально. Откройте страницу учебника с диаграммой
состояния воды, выберите на поле льда диаграммы
любую точку, расположенную выше тройной точки и
ниже критической точки. Опыт проводим при
постоянном давлении, поэтому число факторов n
= 1. Число степеней свободы подсчитываем по
формуле
С = К – Ф + 1.
Нагревание при постоянном давлении на диаграмме состояния выражается передвижением по горизонтальной прямой вправо, в сторону поля жидкости. Эта прямая до пересечения с кривой описывает однофазную однокомпонентную систему с числом степеней свободы:
С = 1 – 1 + 1 = 1.
Это означает, что, изменяя температуру, мы
сохраняем ту же фазу в системе, и она продолжает
оставаться льдом до тех пор, пока прямая не
пересечет кривую зависимости температуры
плавления льда от давления.
Теперь для представления результатов
эксперимента построим график «время –
температура» (рис. 5.12). Пока мы, повышая
температуру, продвигаемся по полю льда, он
нагревается, но не плавится. На этом графике
повышение температуры льда представлено прямой а,
поднимающейся кверху.
Одновременно следите по диаграмме состояния
воды (см. рис. 5.11) за продвижением вдоль прямой по
полю льда к полю жидкой воды. Наконец температура
льда достигла значения на кривой зависимости
температуры плавления от давления. Тогда лед
начинает плавиться, и система становится
двухфазной (лед и жидкость). Число степеней
свободы, относящееся к любой точке этой кривой,
равно:
С = 1 – 2 + 1 = 0.
Здесь система не имеет степеней свободы! Это означает, что, сколько бы тепла ни подводили к смеси воды и льда, температура ее будет оставаться постоянной (0 °С), пока в жидкости будет находиться хоть мельчайший кусочек льда. На графике «время – температура» (см. рис. 5.12) плавление льда представлено горизонтальной прямой б, т. к. система не имеет степеней свободы.
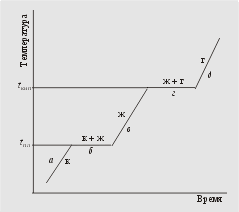 |
Рис. 5.12.
|
В научной литературе такая
горизонтальная линия называется площадкой, она
указывает на постоянство температуры в системе и
отсутствие степеней свободы. Теперь вам понятно,
почему смесь льда и воды нельзя нагреть выше
0 °С?
Наконец весь лед превратился в жидкую воду.
Подводимая в систему теплота расходуется теперь
на нагревание воды. Снова обратитесь к диаграмме
состояния воды. Сейчас мы находимся на поле
жидкой воды и продвигаемся с повышением ее
температуры в сторону поля газа. На графике
«время – температура» появляется прямая в,
поднимающаяся кверху, т. к. температура жидкости
повышается. Это разрешает правило фаз, т. к.
однофазная система имеет одну степень свободы:
С = 1 – 1 + 1 = 1.
Температура системы поднялась до значения, отвечающего пересечению горизонтальной прямой на диаграмме состояния с кривой зависимости давления пара воды от температуры. Началось кипение воды. Система стала двухфазной, с числом степеней свободы снова равным нулю:
С = 1 – 2 + 1 = 0.
На графике «время – температура» появится
горизонтальный участок г, т. е. новая
площадка, и температура 100 °С будет постоянной
до тех пор, пока не испарится (выкипит) последняя
капля жидкости.
Жидкая вода полностью перешла в газ. Подводимая
теплота расходуется на нагревание газообразной
воды. Мы продвигаемся на диаграмме состояния
воды (см. рис. 5.11) по полю газа. Система имеет одну
степень свободы, что на графике отражено
поднимающейся кверху прямой д (см. рис. 5.12).
Если вы поняли, что такое диаграмма состояния, и
увидели, как применяется правило фаз Гиббса, то
самостоятельно сможете разобраться в таких
диаграммах состояния, как, например, «золото –
медь», «золото – серебро» и других более сложных,
которые помогут ответить на вопрос о составах
разнообразных сплавов.
Список новых и забытых понятий и слов
| Фазовый переход; диаграмма состояния воды; поле диаграммы; кривая диаграммы; тройная точка; возгонка, конденсация; критическое состояние, критическое давление, критическая температура; правило фаз Гиббса; степень свободы; компоненты; факторы, влияющие на равновесие. |
О.С.ЗАЙЦЕВ